Chciałbym wrzucić wstępne wyjaśnienie efektu orto do pierścienia:

W badanych cząsteczkach można założyć interakcję między protonami grupy metylowej i wolną parą azotu aminowego oraz ładunkiem ujemnym na karboksylanie.

W pierwszym przypadku gęstość elektronów na atomie N jest (nieznacznie) zmniejszona, a tym samym zasadowość o -toluidyny.

W tym drugim przypadku podobna interakcja zapewnia dodatkową stabilizację karboksylanu. W rezultacie kwas o -toluilowy jest bardziej kwaśny niż izomery.

Chciałbym poprzeć odpowiedź Klausa niektórymi wynikami z kwantowej teorii atomów w cząsteczkach (QTAIM), opartych na obliczeniach DF-BP86 / def2-SVP. Należy zauważyć, że są to wyniki uzyskane bez uwzględnienia solwatacji lub faz skondensowanych. Sądzę, że nadal dowodzą słuszności w przypadku teorii struktury elektronowej.

Powróciłem do tego pytania, aby odpowiedzieć na inne, podobne pytanie. Wkładając w to więcej wysiłku, zdałem sobie sprawę, że traktowane tutaj struktury są w rzeczywistości stanami przejściowymi. Nie oznacza to, że poruszane kwestie są nieważne. Nawet jeśli istnieją tylko przez bardzo krótkie chwile, nadal istnieją i należy je wziąć pod uwagę.

W o -metyloanilinie można wyraźnie zobaczyć sugerowane wewnątrzcząsteczkowe $ \ ce {H} $ obligacja. Odległość $ \ mathbf {d} (\ ce {NH}) = 239,3 ~ \ mathrm {pm} $ jest tylko trochę mniejsza niż suma promieni van der Waalsa, $ \ mathbf {r} (\ ce {N} ) = 155 ~ \ mathrm {pm} $, $ \ mathbf {r} (\ ce {H}) = 110 ~ \ mathrm {pm} $, ale zaniedbanie tego również jest błędne. Nawet jeśli ta interakcja istnieje tylko przez bardzo krótki czas, nadal oznacza, że ​​stabilizuje ten stan. Nie będzie to jednak cecha dominująca.

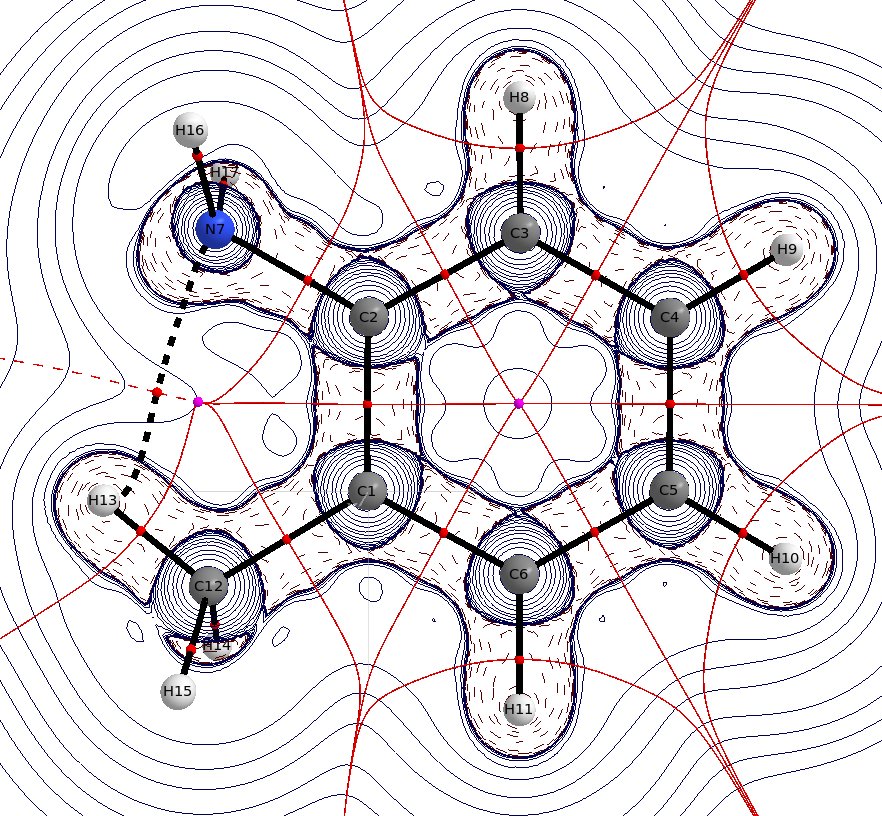
(Rozkład Laplaca, ciągłe niebieskie linie wskazują na wyczerpanie ładunku $ \ nabla ^ 2 \ rho<0 $, przerywane niebieskie linie wskazują akumulację ładunku $ \ nabla ^ 2 \ rho>0 $, Czerwone kule to punkty krytyczne wiązania, fioletowe kule to punkty krytyczne pierścienia, czarne linie to ścieżki wiązania, czerwone linie to powierzchnie o zerowym strumieniu)

Efekty steryczne są zwykle efektami elektronicznymi lub dyspersyjnymi w przebraniu, stąd też odnoszą się do wewnątrzcząsteczkowego wiązania wodorowego. Średnia obligacja $ \ ce {NH} $ wynosi tylko około $ \ mathbf {d} _ \ text {av.} (\ Ce {NH}) \ około 99-105 ~ \ mathrm {pm} $.
Rozwiązanie uwaga użytkownika4604 powinna być nadal brana pod uwagę.

Ta interakcja musi obniżyć powinowactwo do protonów i / lub powinowactwa do kwasu Lewisa, a zatem zmniejsza również zasadowość. Nie tyle dlatego, że jego efekty elektroniczne stabilizują jedną konkretną konformację, ale przede wszystkim sprawiają, że samotna para jest niedostępna przez krótki czas.

Możesz również przeanalizować to pod kątem o -metylobenzoesowy i tutaj efekt zmienia kierunek.
W kwasie benzoesowym jest już pewne wewnątrzcząsteczkowe wiązania wodorowe z orto wodorów, jedno z nich jest nadal obecne w podstawionym przypadku. Odległość $ \ mathbf {d} (\ ce {O-H_ {o '}}) = 226,2 ~ \ mathrm {pm} $ jest tylko trochę mniejsza niż suma promieni van der Waalsa, $ \ mathbf {r} (\ ce {O}) = 151 ~ \ mathrm {pm} $, $ \ mathbf {r} (\ ce {H}) = 110 ~ \ mathrm {pm} $, ale zaniedbanie tego nadal byłoby błędem. Odległość $ \ mathbf {d} (\ ce {O-H_ {Me}}) = 210,8 ~ \ mathrm {pm} $ jest znacznie mniejsza niż suma promieni van der Waalsa. Możesz ponownie zobaczyć interakcję poprzez ścieżkę wiązania i zadzwonić do krytycznych punktów. W zoptymalizowanej geometrii ugrupowanie metylowe jest lekko obrócone, co prowadzi do dwóch równoodległych interakcji. Rotację tej grupy można uznać za swobodną rotację w temperaturze pokojowej.

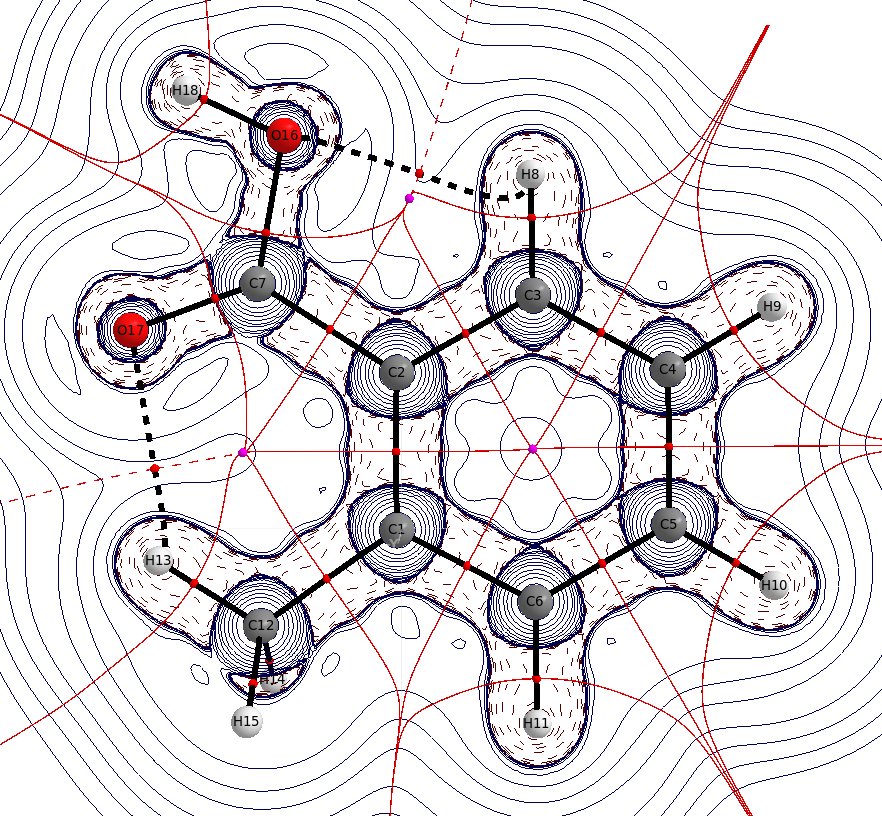
Warto zauważyć, że punkt krytyczny wiązania $ \ ce {O-H_ {kwas}} $ jest prawie w miejscu protonu, co również wskazuje, że większość gęstości elektronów należy już do tlenu.
Jest również oczywiste, że stężenie ładunku w tym wiązaniu jest znacznie niższe niż w jakimkolwiek innym $ \ ce {EX} $ bond, co może wskazywać na słabą więź.

Można to wyjaśnić w inny sposób: o -toluiden jest mniej podstawową przyczyną niż anilinowa z innego powodu. Widzisz, dzieje się tak: kiedy anilina działająca jako zasada staje się $ \ ce {NH3 +} $ (na szczycie pierścienia benzenowego), jest zwykle stabilizowana przez solwatację. Ale jeśli w pozycji orto znajduje się podstawnik, to hamuje on solwatację. W ten sposób zmniejsza się tendencja do zachowywania się jak baza.

W obecności nieporęcznej grupy, którą jest metyl, w tym przypadku powoduje zawadę przestrzenną, powodując, że płaszczyzna $ \ ce {NH3} $ wychodzi z płaszczyzny, zapobiegając w ten sposób rezonansowi, który mógłby pomóc w delokalizacji ładunku +, tworząc w ten sposób podstawę koniugatu bardzo stabilny, ale z powodu przeszkód ładunek + zostaje zlokalizowany i sprawia, że ​​sprzężona zasada jest niestabilna, a więc kwas słabszy.

Ale w przypadku kwasu o-toluilowego, jeśli rysuje się rezonujące struktury sprzężonej zasady, widzimy że pierścień benzenowy wywiera efekt + m (mezomeryczny), co nie ma miejsca w przypadku o-toluidyny, która rzeczywiście jest odwrotnie proporcjonalna do mocy kwasowej, a zatem niepłaski spowodowany przez SIR jest teraz korzystny dla podstawnika, czyniąc go wolnym od + M efekt pierścienia i tym samym zwiększenie jego kwasowości. Teraz podstawnik może swobodnie tworzyć równoważny rezonans, który może wspierać kwasowość i nie zostanie uszkodzony przez pierścienie + M.

Użytkownik4604 ma poprawną wartość z argumentem rozwiązywania.

Innymi słowy, kwasowość i zasadowość tych kompleksów są zwykle mierzone w wodzie, gdzie energia swobodna hydratacji naładowanych cząsteczek może być bardzo wysoka (tj. korzystne jest rozpuszczanie naładowanych cząsteczek). Jeśli podstawniki niepolarne zostaną umieszczone w pobliżu naładowanej grupy, zapobiegnie to skutecznemu oddziaływaniu i solwatacji tej naładowanej grupy z wodą. W ten sposób niepolarny podstawnik wpłynie na pKa (zasadowość i kwasowość) naładowanej grupy. To, czy grupa niepolarna sprawia, że ​​ugrupowanie jest bardziej zasadowe, czy kwaśne, zależy od konkretnego przypadku (kwas 2-metylobenzoesowy będzie bardziej zasadowy / mniej kwaśny niż kwas 4-metylobenzoesowy; jednak 2-metyloanilina będzie mniej zasadowa / bardziej kwaśna niż 4- metyloanilina).

Przeanalizowałem problem w inny sposób. Basicity implikuje tendencję do protonowania. W pierwszym przypadku grupa metylowa wywołuje zawadę przestrzenną i zapobiega protonowaniu, co z kolei czyni ją mniej zasadową w porównaniu z aniliną. Z drugiej strony w drugim przypadku rozważmy moc kwasową orto podstawionych i niepodstawionych prawie równych, ale z powodu zawady sterycznej ponownie, tendencja do utraty elektronów jest bardziej niepodstawiona, co czyni ją mniej kwaśną w porównaniu z podstawioną. natura.